Gradient Descent en Español - Python

Implementación del Algoritmo de Gradient Descent

En este notebook, implementaremos las funciones básicas del algortimo de Gradient Descent para encontrar el límite de un pequeño dataset. Primero, empezaremos con unas funciones que nos ayudarán a visualizar mejor los datos.

#Importar las módulos necesarios

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

#Algunas funciones de ayuda para trazar gráficos y lineas

def trazar_puntos(X, y):
    admitted = X[np.argwhere(y==1)]
    rejected = X[np.argwhere(y==0)]
    plt.scatter([s[0][0] for s in rejected], [s[0][1] for s in rejected], s = 25, color = 'blue', edgecolor = 'k')
    plt.scatter([s[0][0] for s in admitted], [s[0][1] for s in admitted], s = 25, color = 'red', edgecolor = 'k')

def mostrar(m, b, color='g--'):
    plt.xlim(-0.05,1.05)
    plt.ylim(-0.05,1.05)
    x = np.arange(-10, 10, 0.1)
    plt.plot(x, m*x+b, color)

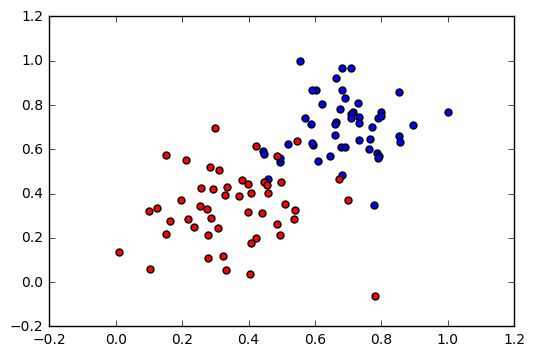
Leer y trazar los datos

data = pd.read_csv('/data.csv', header=None)
print(data.head())
X = np.array(data[[0,1]])
y = np.array(data[2])
trazar_puntos(X,y)
plt.show()

         0         1  2
0  0.78051 -0.063669  1
1  0.28774  0.291390  1
2  0.40714  0.178780  1
3  0.29230  0.421700  1
4  0.50922  0.352560  1

Para hacer: Implementar funciones básicas

Implementar las siguientes formulas:

• Función de activación Sigmoid

\[\sigma(x) = \frac{1}{1+e^{-x}}\]

• Fórmula de Salida (predicción)

\[\hat{y} = \sigma(w_1 x_1 + w_2 x_2 + b)\]

• Fórmula de Función de Error

\[Error(y, \hat{y}) = - y \log(\hat{y}) - (1-y) \log(1-\hat{y})\]

• Fórmula de la función que actualiza los pesos

\[w_i \longrightarrow w_i + \alpha (y - \hat{y}) x_i\] \[b \longrightarrow b + \alpha (y - \hat{y})\]

# Implementar las siguientes funciones

# Función de axctivación Sigmoid

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

#Fórmula de Salida (predicción)

def formula_salida(caracteristicas, pesos, prejuicios):
    return sigmoid (np.dot(caracteristicas, pesos) + prejuicios)

# Fórmula de error (log-perdida)

def formula_error(y, salida):
    return -y*np.log(salida)-(1-y)* np.log(1 - salida)

# Paso Gradient Descent

def actualizar_pesos(x, y, pesos, prejuicios, velocidadaprendizaje):
    salida = formula_salida(x, pesos, prejuicios)
    d_error = y - salida
    pesos += velocidadaprendizaje * d_error
    prejuicios += velocidadaprendizaje * d_error
    return pesos, prejuicios

Entrenar la función

Esta función nos ayudara a iterar el algoritmo Gradient Descent a travez de todos los datos por un cierto numero de epochs. Tambien trazará los datos y algúnos de las líneas de límites las cuales se obtienen mientras se ejecuta el algoritmo.

np.random.seed(44)

epochs = 100
velocidadaprendizaje = 0.01

def entrenar(caracteristicas, targets, epochs, velocidadaprendizaje, graph_lines=False):
    
    errores = []
    n_records, n_caracteristicas = caracteristicas.shape
    last_perdida = None
    pesos = np.random.normal(scale=1 / n_caracteristicas**.5, size=n_caracteristicas)
    prejuicios = 0
    for e in range(epochs):
        del_w = np.zeros(pesos.shape)
        for x, y in zip(caracteristicas, targets):
            salida = formula_salida(x, pesos, prejuicios)
            error = formula_error(y, salida)
            pesos, prejuicios = actualizar_pesos(x, y, pesos, prejuicios, velocidadaprendizaje)
        
        # Imprimir el error log-perdida del grupo de entrenamiento
        
        salida = formula_salida(caracteristicas, pesos, prejuicios)
        perdida = np.mean(formula_error(targets, salida))
        errores.append(perdida)
        if e % (epochs / 10) == 0:
            print("\n========== Epoch", e,"==========")
            if last_perdida and last_perdida < perdida:
                print("Pérdida en Entrenamiento: ", perdida, "  ADVERTENCIA - Pérdida Incrementando")
            else:
                print("Pérdida en Entrenamiento: ", perdida)
            last_perdida = perdida
            predicciones = salida > 0.5
            exactitud = np.mean(predicciones == targets)
            print("exactitud: ", exactitud)
        if graph_lines and e % (epochs / 100) == 0:
            mostrar(-pesos[0]/pesos[1], -prejuicios/pesos[1])
            

    # Gráfico del límite de la solución
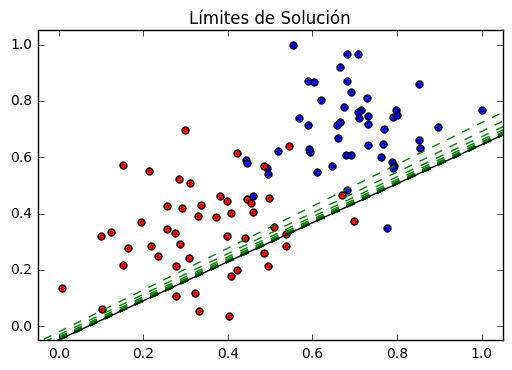
    plt.title("Límites de Solución")
    mostrar(-pesos[0]/pesos[1], -prejuicios/pesos[1], 'black')

    # Gráfico de los datos
    trazar_puntos(caracteristicas, targets)
    plt.show()

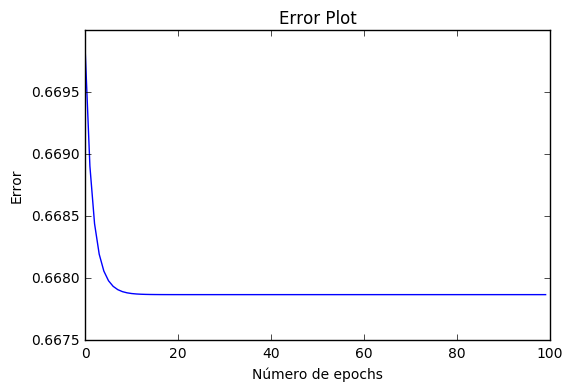
    # Gráfico del error
    plt.title("Gráfico de Error")
    plt.xlabel('Número de epochs')
    plt.ylabel('Error')
    plt.plot(errores)
    plt.show()

Hora de entrenar al algoritmo!

Cuando ejecutamos la función, obtenemos lo siguiente:

• 10 actualizaciones con los valores actuales de la pérdida y exactitud
• Un gráfico de los datos con líneas de límite. El último es en negro. Fíjate en como las lineas se acercan a una mejor aproximacioón en cada epoch.
• Un gráfico de la función de error. Fíjate en como su valor disminuye mientras avanzan en mas epochs.

#Llamar la función de entrenamiento 
entrenar(X, y, epochs, velocidadaprendizaje, True)

========== Epoch 0 ==========
Pérdida en Entrenamiento:  0.6698236771939231
exactitud:  0.6

========== Epoch 10 ==========
Pérdida en Entrenamiento:  0.6678746196991412
exactitud:  0.6

========== Epoch 20 ==========
Pérdida en Entrenamiento:  0.667865938509054
exactitud:  0.6

========== Epoch 30 ==========
Pérdida en Entrenamiento:  0.6678658823869832
exactitud:  0.6

========== Epoch 40 ==========
Pérdida en Entrenamiento:  0.6678658820231004
exactitud:  0.6

========== Epoch 50 ==========
Pérdida en Entrenamiento:  0.667865882020741
exactitud:  0.6

========== Epoch 60 ==========
Pérdida en Entrenamiento:  0.6678658820207256
exactitud:  0.6

========== Epoch 70 ==========
Pérdida en Entrenamiento:  0.667865882020725
exactitud:  0.6

========== Epoch 80 ==========
Pérdida en Entrenamiento:  0.6678658820207246
exactitud:  0.6

========== Epoch 90 ==========
Pérdida en Entrenamiento:  0.6678658820207243
exactitud:  0.6